|
Примеры решений дифференциальных уравнений
Решаем дифференциальное уравнение:

Произведем нормировку уравнения. Разделим все уравнение на коэффициент при y'. Получим:

Вычисляем вспомогательную фунцию:

Вычисляем:


Согласно теории по данному типу диффуров, записываем выражение:



Интегрируем левую и правую часть. Получим:


Выразим искомую функцию y(x):

Записываем финальный ответ:

Выполним проверку. Подставим полученную функцию y(x) в исходный диффур.
Упрощаем:

Значение правой части диффура:

Выражения должны быть математически идентичны (с точностью до формы записи).
|
Решаем дифференциальное уравнение:

Произведем нормировку уравнения. Разделим все уравнение на коэффициент при y'. Получим:

Разделим все уравнение на y2. Получили:

Делаем замену переменных.


Тогда уравнение можно записать как:

Получили линейное неоднородное уравнение первого порядка. Решим его.
-
Решаем дифференциальное уравнение:

Вычисляем вспомогательную фунцию:

Вычисляем:


Согласно теории по данному типу диффуров, записываем выражение:



Интегрируем левую и правую часть. Получим:


Выразим искомую функцию w(x):

Записываем решение уравнения:

|
Зная w(x) найдем y(x):

Записываем финальный ответ:

Выполним проверку. Подставим полученную функцию y(x) в исходный диффур.
Упрощаем:

Выражение, записанное выше, это то, что получится при подстановке y(x) в левую часть диффура.
А теперь посмотрим что получится при подстановки y(x) в правую часть диффура:

Упрощаем:

Выражения должны быть математически идентичны (с точностью до формы записи).
|
- Решаем дифферениальное уравнение:

Упростим выражение, собрав коэффициенты при dx и dy:

Обозначим через P(x,y) коэффициент при dx

Обозначим через Q(x,y) коэффициент при dy

Проверяем равенство:




Равенство (2) выполняеться, значит уравнение (1) - это уравнение в полных дифференциалах
Ответ ищем в виде функции  : :



Предварительный ответ уже получили, надо найти функцию 
Вспоминаем, что:

где


Запишем равенство (3) в явном виде

Выразим функцию 



Финальный ответ

|

- Решаем однородное дифференциальное уравнение:

Решение ищем в виде:

Подставляем в исходное уравнение:

Дифференцируем экспоненту, а затем сокращаем на exp(x·z). Получим характерестическое уравнение:

Решаем характерестическое уравнение. Получим два корня:


Корни представляют собой два одинаковых действительных числа. Тогда фундаментальная система решений однородного дифференциального уравнения представляет собой две функции:


где С1 и С2 произвольные константы.
Общее решение однородного дифференциального уравнения представляет собой сумму фундаментальных решений:


Раскладываем и группируем (если это возможно) слагаемые в правой части таким образом, чтобы удобнее было решать:
Решаем дифференциальное уравнение:

Частное решение данного уравнения:

показать решение
Анализируем правую часть неоднородного уравнения:
Максимальная степень полиномов 1.
Решение ищем в виде функции yHP (HP - неоднородное решение):

Основная задача теперь звучит так: надо найти неизвестные коэффициенты c1,c0.
Подставляем yHP вместо y в левой части исходного дифференциального уравнения и дифференцируем. После дифференцирования получили:


Полученное выражение будем называть yHP подстава.
Приравниваем yHP подстава к правой части исходного диффура:

Из этого выражения попробуем определить неизвестные коэффициенты c1,c0.
Сгруппируем слагаемые в yHP подстава по степеням х :


Сгруппируем слагаемые правой части уравнения по степеням х :


Собираем коэффициенты ( это то, что в квадратных скобках)
при одинаковых множителях (это exp,степень x) от yHP подстава
и от правой части диффура. Получим линейную систему уравнений:

Решаем данную систему, получили следующие значения:


Вспоминаем как мы определили yHP и подставляем туда значения c1,c0.

Делаем проверку.
Подставим yHP в исходный диффур и продиффиренцируем. Дожно получиться выражение стоящее справо от знака равенста.
После подстановки yHP в диффур мы получили:

Исходное значение правой части диффура:

Выражения должны быть идентичны.
|
Решаем дифференциальное уравнение:

Частное решение данного уравнения:

показать решение
Анализируем правую часть неоднородного уравнения:
Максимальная степень полиномов 0.
Решение ищем в виде функции yHP (HP - неоднородное решение):

Основная задача теперь звучит так: надо найти неизвестные коэффициенты c0,s0.
Подставляем yHP вместо y в левой части исходного дифференциального уравнения и дифференцируем. После дифференцирования получили:


Полученное выражение будем называть yHP подстава.
Приравниваем yHP подстава к правой части исходного диффура:

Из этого выражения попробуем определить неизвестные коэффициенты c0,s0.
Сгруппируем слагаемые в yHP подстава по степеням х :


Сгруппируем слагаемые правой части уравнения по степеням х :


Собираем коэффициенты ( это то, что в квадратных скобках)
при одинаковых множителях (это exp, sin, cos, степень x) от yHP подстава
и от правой части диффура. Получим линейную систему уравнений:

Решаем данную систему, получили следующие значения:


Вспоминаем как мы определили yHP и подставляем туда значения c0,s0.

Делаем проверку.
Подставим yHP в исходный диффур и продиффиренцируем. Дожно получиться выражение стоящее справо от знака равенста.
После подстановки yHP в диффур мы получили:

Исходное значение правой части диффура:

Выражения должны быть идентичны.
|
Записываем финальный ответ:

|
- Решаем дифференциальное уравнение:
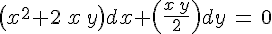
Уравнение однородное, порядок уравнения 2.
Сделаем ряд преобразований:
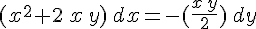
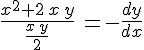
Приведем уравнение к виду:
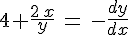
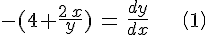
Вводим новую функцию z(x):
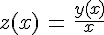
Тогда:
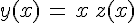
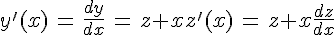
В уравнении (1) делаем замену:
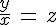
и
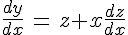
Получим:
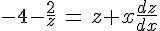
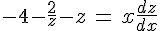
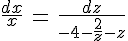
Интегрируем:
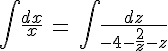
Получим:
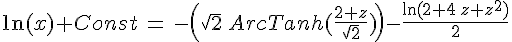
Делаем обратную замену:
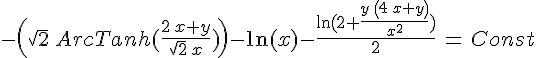
|
|